- Methodology
- Open access
- Published:
PopMod: a longitudinal population model with two interacting disease states
Cost Effectiveness and Resource Allocation volume 1, Article number: 6 (2003)
Abstract
This article provides a description of the population model PopMod, which is designed to simulate the health and mortality experience of an arbitrary population subjected to two interacting disease conditions as well as all other "background" causes of death and disability. Among population models with a longitudinal dimension, PopMod is unique in modelling two interacting disease conditions; among the life-table family of population models, PopMod is unique in not assuming statistical independence of the diseases of interest, as well as in modelling age and time independently. Like other multi-state models, however, PopMod takes account of "competing risk" among diseases and causes of death.
PopMod represents a new level of complexity among both generic population models and the family of multi-state life tables. While one of its intended uses is to describe the time evolution of population health for standard demographic purposes (e.g. estimates of healthy life expectancy), another prominent aim is to provide a standard measure of effectiveness for intervention and cost-effectiveness analysis. PopMod, and a set of related standard approaches to disease modelling and cost-effectiveness analysis, will facilitate disease modelling and cost-effectiveness analysis in diverse settings and help make results more comparable.
Introduction
Historical background and analytical context
Measuring population health has been inseparable from the modelling of population health for at least three hundred years. The first accurate empirically based life table – a population model, albeit a simple one – was constructed by Edmund Halley in 1693 for the population of Breslau, Germany.[1] However, the 1662 life table of John Graunt, while less rigorously based on empirical mortality data, represented a reasonably good approximation of life expectancy at birth in the seventeenth century.[2] Indeed, because of Graunt's strong a priori assumptions about age-specific mortality, his life table could be said to represent the first population model. Recently, multi-state life tables, which explicitly model several population transitions, have become a common tool for demographers, health economists and others, and a considerable body of theory has been developed for their use and interpretation.[3–5] Despite the substantial complexity of existing multi-state models, a recent publication has highlighted the advantages of so-called "dynamic life tables", in which age and time would be modelled independently.[6]
Mathematical and computational constraints are no longer serious obstacles to solving complex modelling problems, although the empirical data required for complex models are. In particular, multi-state models present data requirements that can rapidly exceed empirical knowledge about real-world parameter values, and in many cases, the input parameters for such models are therefore subject to uncertainty. Nevertheless, even with substantial uncertainty, such models can provide robust answers to interesting questions. Indeed, the work of John Graunt demonstrates the practical value of results obtained with even purely hypothetical parameter values.
PopMod, one of the standard tools of the WHO-CHOICE programme http://www.who.int/evidence/cea, is the first published example of a multi-state dynamic life table. Like other multi-state models, PopMod takes account of "competing risk" among diseases, causes of death and possible interventions. However, PopMod represents a new level of complexity among both generic population models and the family of multi-state life tables. Among population models with a longitudinal dimension, PopMod is unique in modelling two distinct and possibly interacting disease conditions; among the life-table family of population models, PopMod is unique in not assuming statistical independence of the diseases of interest, as well as in modelling age and time independently.
While one of PopMod's intended uses is to describe the time evolution of population health for standard demographic purposes (e.g. estimates of healthy life expectancy), another prominent aim is to provide a standard measure of effectiveness for intervention and cost-effectiveness analysis. PopMod, and a related set of standard approaches to disease modelling and cost-effectiveness analysis used in the WHO-CHOICE programme, facilitate disease modelling and cost-effectiveness analysis in diverse settings and help make results more comparable. However, the implications of a tool such as PopMod for intervention analysis and cost-effectiveness analysis is a relatively new area with little published scholarship. Most published cost-effectiveness analysis has not taken a population approach to measuring effectiveness, and when studies have done so they have generally adopted a steady-state population metric.[7] Relatively little published research has noted the biases of conventional approaches when used for resource allocation.[8]
Despite similarities in some of the mathematical techniques,[9] this paper does not consider transmissible disease modelling.
Basic description of the model
PopMod simulates the evolution in time of an arbitrary population subject to births, deaths and two distinct disease conditions. The model population is segregated into male and female subpopulations, in turn segmented into age groups of one-year span. The model population is truncated at 101 years of age. The population in the first group is increased by births, and all groups are depleted by deaths. Each age group is further subdivided into four distinct states representing disease status. The four states comprise the two groups with the individual disease conditions, a group with the combined condition and a group with neither of the conditions. The states are denominated for convenience X, C, XC and S, respectively. The state entirely determines health status and disease and mortality risk for its members. For example, X could be ischaemic heart disease, C cerebrovascular disease, XC the joint condition and S the absence of X or C.
State members undergo transitions from one group to another, they are born, they get sick and recover, and they die. The four groups are collectively referred to as the total population T, births are represented as the special state B, and deaths as the special state D. A diagram for the first age group is shown in Figure 1 (notation used is explained in the section Describing states, populations and transitions between states). In the diagram, states are represented as boxes and flows are depicted as arrows. Basic output consists of the size of the population age-sex groups reported at yearly intervals. From this output further information is derived. Estimates of the severity of the states X, C, XC and S are required for full reporting of results, which include standard life-table measures as well as a variety of other summary measures of population health.
There now follows a more technical description of the model and its components, broken down into the following sections: describing states, populations and transitions between states; disease interactions; modelling mechanics; and output interpretation. The article concludes with a discussion of the relation of PopMod to other modelling strategies, plus a consideration of the implications, advantages and limitations of the approach.
Describing states, populations and transitions between states
Describing states and populations
In the full population model depicted in Figure 1, six age-and-sex specific states (X, C, XC, S, B and D) are distinguished. However, births B and deaths D are special states in the sense that they only feed into or absorb from other states (while the states X, C, XC and S both feed into and absorb from other states). Special states are not treated systematically in the following, which focuses on the "reduced form" of the model consisting of the states X, C, XC, and S.
States are not distinguished from their members; thus, "X" is used to mean alternatively "disease X" or "the population group with disease X", according to context. The second meaning is equivalent to the prevalence count for the population group.
For the differential equation system, states/groups are always denoted in the strict sense: "X" means "state X only" or "the population group with only X". However, in deriving input parameters (described more fully below in the section Disease interactions) from observed populations, it is convenient to describe groups in a way that allows for the possibility of "overlap". For example in Figure 2, the area "X" might be understood to mean either "the population group with X including those members with C as well" (i.e. the entire circle X) or the "the population group with only X" (i.e. the circle minus the region overlapping with circle C).
Since these two valid meanings imply different uses of notation, the following conventions are adopted:
-
The differential equations expressions X, C, XC and S refer only to disjoint states (or groups).
-
The logical operator "~ "means "not", thus "~ X" is the state "not X" (or "the group without X").
-
The logical expressions denoted in the left-hand column of Table 1 have the meaning and alternative description indicated in the two right-hand columns.
Prevalence rates (p) describe populations (i.e. prevalence counts) as a proportion of the total, for example:
p X = X/T, p C = C/T, p XC = XC/T, p S = S/T. (1)
Here, prevalence is presented in terms of the disjoint populations X, C and XC, and the notation from the right-hand column of Table 1 is used. In the section Disease interactions, we discuss the case of overlapping populations.
A prevalence rate is always interpretable as a probability, but a probability is not always interpretable as a prevalence. The lower-case Greek letter pi (π) is used throughout this article to denote probability. Probabilities can be used to describe populations as noted in Table 2.
Describing transitions between states
In the differential equation system, transitions (i.e. flows) between population groups are modelled as instantaneous rates, represented in Figure 1 as labelled arrows. Instantaneous rates are frequently called hazard rates, a usage generally adopted here (demographers tend to refer to instantaneous rates as "hazards" or as "forces" – e.g. force of mortality – although epidemiologists commonly use the term "rate" with the same meaning). A transition hazard is labelled here h, frequently with subscript arrows denoting the specific state transition.
In PopMod terminology, the transitions X→D, C→D and XC→D are partitioned into two parts, one of which is the cause-specific fatality hazard f due to the condition X, C or XC, and the other which is the non-specific death hazard (due to all other causes), called background mortality m:
h X→D = f X + m (2a)
h C→D = f C + m (2b)
h XC→D = f XC + m (2c) (2)
h S→D = m. (2d)
PopMod consequently allows for up to twelve exogeneous hazard parameters (Table 3).
Transition hazards
A time-varying transition hazard is denoted h(t). The hazard expresses the proportion of the at-risk population (dP/P) experiencing a transition event (i.e. exiting the population) during an infinitesimal time dt:
h(t) = - (1/P)·dP/dt. (3)
"Instantaneous rate" means the transition rate obtaining during the infinitesimal interval dt, that is, during the instant in time t. If an instantaneous rate does not vary, or its small fluctuations are immaterial to the analysis, PopMod parameters can be interpreted as average hazards without prejudice to the model assumptions.
Average hazards can be approximated by counting events ΔP during a period Δt and dividing by the population time at risk. If for practical purposes the instantaneous rate does not change within the time span, the approximate average hazard can be used as an estimate for the underlying instantaneous rate:
-
(1/P)·dP/dt ≈ -∫dP / ∫P dt ≈ - ΔP / (P·Δt), (4)
where ΔP = ∫dP is the cumulative number of events occurring during the interval Δt, and ∫P dt ≈ P·Δt is the corresponding population time at risk. Time at risk is approximated by multiplying the mid-interval population (P) by the length of the interval Δt.
For example, if ten deaths due to disease X (ΔP = 10) occur in a population with approximately one million years of time at risk (P·Δt = 1,000,000), an approximation of the instantaneous rate h X→D (t) is given by:
h X→D (t) ≈ ΔP / P·Δt = 10 / 1,000,000 = 0.00001. (5)
Note that while eq. (3) and eq. (4) are equivalent in the limit where Δt→0, the approximation in eq. (4) will result in large errors when rates are high. This is discussed in the section Proportions and hazard rates, and an alternative formula for deducing average hazard is proposed in eq. (9).
The quantity in eq. (4) has units "deaths per year at risk", and is often called a "cause-specific mortality hazard". For the same population and deaths, but restricting attention to the group with disease X (where, for example, P·Δt = 10,000) the calculated hazard will be larger:
h X→D (t) ≈ ΔP / P·Δt = 10 / 10,000 = 0.001. (6)
The quantity in eq. (6) has the same units as that in eq. (5), but is a "case fatality hazard". Note that the same transition events (e.g. "dying of disease X") can be used to define different hazard rates depending on which population group is considered.
Proportions and hazard rates
Integration by parts of eq. (3) shows that the proportion of the population experiencing the transition in the time interval Δt (i.e. the "incident proportion") is given by:

If the hazard is constant, that is, if h(t) = h(t 0) = h, ∫dt = Δt and the integral collapses. The incident proportion is then written:

The incident proportion can always be interpreted as the average probability that an individual in the population will experience the transition event during the interval (e.g. for mortality, this probability can be written πP→D = ΔP/P). The qualification "average" is dropped if individuals in P are homogeneous with respect to transition risk during the interval.
Even if the hazard is not constant, eq. (8) can be rearranged to give an alternative (exact) formula for calculating the equivalent constant hazard h yielding ΔP transitions in the interval Δt:

However, if the true hazard is constant during the interval, the "equivalent constant hazard" equals the "average hazard" and the "instantaneous rate". The same identity applies when fluctuations in the underlying hazard are of no practical importance. PopMod requires the assumption that hazards are constant within the unit of its standard reporting interval, defined by convention as one year.
Note that series expansion of exp{-h·Δt} or ln{1-ΔP/P} shows that, for values of h·Δt << 1 and ΔP/P << 1, the equivalent constant hazard is well approximated by the time-normalized incident proportion, and vice versa, as in eq. (4):

Case-fatality hazards
Case-fatality hazards f X, f C, and f XC are defined with respect to the specific populations X, C and XC, respectively:

Mortality hazards
Mortality hazards are defined with respect to the entire population, where cause-specific mortality hazards are conditional on cause of death:

The background mortality rate m is defined as the instantaneous rate of deaths due to causes other than X or C.
Disease interactions
PopMod is typically used to simulate the evolution of a population subjected to two disease conditions, where health status, health risk and mortality risk are conditional on disease state. Health status, health risk and mortality risk are plausibly conditional on disease state when the two primary disease conditions X and C interact. Such interactions can be analysed from various perspectives, for example, common risk factors, common treatments, common prognosis; however, the primary perspective adopted here for the pupose of analysis is that of "common prognosis", by which is meant that the two conditions mutually influence prevalence, incidence, remission and mortality risk.
A previously cited example was that of ischaemic heart disease (X) and cerebrovascular disease (C): it is well known that individuals with either heart disease or stroke history have lower health status and higher mortality risk than individuals with neither of these conditions, and that individuals with heart disease are at increased risk for stroke and vice versa.
Furthermore, individuals with history of both heart disease and stroke (XC) are known to have higher mortality risk and lower health status than either individuals with only one of the disease histories or those with neither. However, in this example as in many others, information about the joint condition (heart disease and stroke) is scarce relative to information about the two individual conditions (heart disease or stroke). The obvious reason for this is that the population group with the joint condition is smaller in size and has a lower life expectancy, reducing opportunities for data collection.
The presimulation problem
One of PopMod's guiding principles, therefore, is that while an analyst has access to information about basic parameter values for the conditions X and C (i.e. prevalence rates and incidence, remission and either case-fatality or cause-specific mortality hazards), the same is not generally true for the joint condition XC. Thus, more or less by construction, the modelling situation is one in which data for the joint condition are scarce or unavailable, and must consequently be derived from data known for the individual conditions.
An important implication is that the data available for the individual conditions (X and C) will be reported in terms of overlapping populations. Where specifically noted, therefore, the notation in the left-hand column of Table 1 (Logical expressions) is used in the following, with the particular implication that "X", for example, means "the population group with X including those members with C as well" (i.e. "X + XC" in differential equations terminology).
Once parameter values for the joint condition are determined, the minimum set of parameters required for population simulation are known. The parameter-value problem – referred to here as the presimulation problem, since its solution must precede population simulation per se – can be divided into two principal parts: one concerning the prevalence rates defining the intial conditions (stocks) of the differential equations system, and the other the transition hazards defining its flows. These stocks and flows together make up the initial scenario of the population model. A cross-sectional approach is adopted in which deriving these two kinds of parameters values for the initial scenario are treated as separate problems.
The analytics of these derivations largely depend on which of a range of possible assumptions is made about the interactions of the two principal conditions. The simplest possible assumption is essentially an assumption of non-interaction (statistical independence). Since an understanding of the non-interacting case is an essential starting point for more complex interactions, it is discussed first.
The independence assumption
Prevalence for the joint group
When conditions X and C are statistically independent, the joint prevalence is the product of the individual (marginal) prevalences:
p XC = p X·p C. (17)
Transition hazards for the joint group
Independence implies that the hazards for the group with X or C are equal to the corresponding hazards for the group without X or C (in eq. (18) populations are denoted in differential equations (disjoint) notation from the right-hand column of Table 1):
h XC→C = h X→S
h XC→X = h C→S (18)
h C→XC = h S→X
h X→XC = h S→C
Joint case fatality hazard
The probabilities

and  for an individual in group X or C to die of cause X or C, respectively, during an interval Δt are:
for an individual in group X or C to die of cause X or C, respectively, during an interval Δt are:

So the joint probability

for someone in the group XC dying of either X or C is given by the laws of probability:

Although individuals in the joint group XC are at risk of death from either X or C, or from other causes, the probability framework requires the assumption that they do not die of simultaneous causes (i.e. there is no cause of death "XC").
The combined case-fatality rate f XC is thus:
f XC = f X + f C. (21)
This simple addition rule can be generalized to situations with more than two independent causes of death.
Background mortality hazard
The "background mortality hazard" m expresses mortality risk for population T due to any cause of death other than X and C. The "independence assumption" claims m is independent of these causes, in other words, that m acts equally on all groups (in eqs. (22–25) populations are denoted in differential equations notation from the right-hand column of Table 1):
m·T = m·(S + X + C + XC) = m·S + m·X + m·C + m·XC. (22)
The total ("all cause" or "crude") death hazard for the population is written m tot. The following identity expresses the constraint that deaths in population T equal the sum of deaths in populations S, X, C and XC:
m tot·T = m·S + (m + f X)·X + (m + f C)·C + (m + f XC)·XC. (23)
Thus:
m tot·T = m·(S + X + C + XC) + f X·X + f C·C + f XC·XC
= m·T + f X·X + f C·C + (f X + f C)·XC (24)
=m·T + f X·(X + XC) + f C·(C + XC).
Since by definition group X or C contributes no deaths due to cause C or X, respectively:
f C·(C + XC) = m C·T,
f X·(X + XC) = m X·T, (25)
so:
m tot·T = m·T + m X·T + m C·T. (26)
and:
m = m tot - m X - m C. (27)
Likewise, this rule is generalizable to scenarios with more than three (m, X, C) independent causes of death.
Relaxing the independence assumption
As noted in the introduction, one of the primary reasons for the introduction of PopMod was to model disease interactions in a longitudinal population model. Modelling interactions requires relaxing the assumption of independence.
In the presimulation of the "stocks and flows" required for the initial scenario, three areas of interaction for the health states X and C can be distinguished. Having X (C) may make it more or less likely to:
-
(1)
have C (X),
-
(2)
acquire or recover from C (X),
-
(3)
die from C (X).
Note that while interaction (1) could alternatively be considered the cumulative result of interactions (2) and (3) in the past, this is not the approach adopted here.
Interaction (1): Prevalence of the joint group
In this and subsequent sections except where noted, we revert to the notation from the left-hand column of Table 1. Table 4 shows six possible cases for calculating prevalence of the joint group depending on the type of information known about the disease interaction. The probability notation π is used for prevalence, where πX|C is the probability of having disease X among those who have disease C and πX and πC are short forms for πX|T and πC|T. Relative risk (RR) is defined here as a ratio of probabilities (risk ratio), for example, RRC|X = πC|X / πC|~X is the probability of having X if C is present over the probability of having X if C is not present.
Calculations for case 1 follow directly from the assumption of independence. Cases 2 and 3 follow directly from the definition of conditional probability. Cases 4 and 5 are derived as follows. Since the probability of belonging to the joint group is independent of which disease group is conditioned on, it is clear that:
π XC = π X|C ·π C = π C|X ·π X . (28)
Using the definition of conditional probability, we write:
π X = π X|C ·π C + π X|~C ·π~C , and
π C = π C|X ·π X + π C|~X ·π~X . (29)
Now supposing RRX|C or RRC|X is known, solving either for πX|C or πC|X and substituting the result into eq. (29) and solving again for πX|C and πC|X yields:
π X|C = π X / (π C + π~C / RR X|C ), and
π C|X = π C / (π X + π~X / RR C|X ). (30)
So again using the definition of conditional probability:
π XC = π X ·π C / (π C + π~C / RR X|C ), and
πXC = π C ·π X / (π X + π~X / RR C|X ). (31)
Recalling 1 - πX = π~X and 1 - πC = π~C, the required expressions in Table 4 are obtained.
The factor k in case 6 is an arbitrary multiplier that increases or reduces the prevalence of group XC compared to what would be obtained under independence, and lies between 0 and 1 if having one disease reduces the probability of having the other, and between 1 and MAX(1/πC, 1/πX) if having one disease makes it more likely to have the other. Upper bounds on k are easy to derive using the fact that πXC = πX = πC when X and C are obligate symbiotes.
The six cases span a range of information availability about interaction of X and C on the prevalence of the joint condition:
-
Case 1 assumes independence (no interaction).
-
Case 2 and 3 assume conditional prevalence is known.
-
Case 4 and 5 assume relative risk is known.
-
Case 6 assumes a potentiation (or protection) factor can be defined.
Interaction (2): Incidence and remission for the joint group
For incidence hazard, we write i and for remission hazard, r. Consistent with "overlapping populations", unless specifically noted, hazards are understood as "total hazards", that is, i X includes all incidence to X regardless of whether C is also present in the population at risk. Conditional hazards are denoted i X|~C or i X|C to signify "incidence to X in the group without C" and "incidence to X in the group with C", respectively.
Consider total incidence i X for the initial scenario. The product of total incidence to X and the total population without X (~X) must be equal to the sum of the products of the conditional incidences (i X|~C, i X|C) and the conditional populations (~X~C, ~XC):
i X·(~X) = i X|~C·(~X~C) + i X|C·(~XC). (32)
Dividing by total population T yields:

and replacing population ratios by the corresponding prevalence rates yields:
i X·π~X = i X|~C·π~X~C + i X|C·π~XC. (34)
Dividing both sides by π~X yields the following expression for i X:

where:
π~X = π~X~C + π~XC. (36)
It is therefore clear that total incidence to X is a weighted average of the conditional incidences, where the weights are the proportions of the population without X partitioned according to C status.
Recall that, in terms of the differential equations notation from the right-hand column of Table 1, π~X = πC + πS, π~X~C = πS and π~XC = πC, the values of which are determined according to one of the six cases defined above in interaction (1). Thus, when total hazard i X is known, eq. (34) has only two unknowns (i X|~C and i X|C). Clearly, if information on one or both conditional hazards is available, interaction (2) with respect to i X is fully characterized for the initial scenario.
However, the guiding principle of the presimulation problem was that information on the non-overlapping populations (e.g. direct observation of the conditional hazards) is relatively scarce. When this is true, the unknown conditional hazards must remain undetermined unless one of the following three rate ratios (RR) is known or can be approximated:

A similar situation applies to the total hazards i C, r C, and r X for the initial scenario, that is, eq. (34) is one of a family of equations representing the relation between the total disease hazards and the corresponding conditional hazards for subpopulations:
i X·π~X = i X|~C·π~X~C + i X|C·π~XC
i C·π~C = i C|~X·π~X~C + i C|X·πX~C (38)
r X·πX = r X|~C·πX~C + r X|C·πXC
r C·πC = r C|~X·π~XC + r C|X·πXC.
Note that, with respect to the initial scenario, eq. (38) forms a simultaneous system with eq. (31) – or one of the other methods of calculating πXC noted in Table 4 – and the system has a unique numerical solution whenever enough parameter values are known, that is, assuming the four total hazards are known, if one of the three following rate ratios (or its inverse) is known for each hazard:

Interaction (3): Mortality for the joint group
This interaction concerns causes of death. We assume that the all-cause mortality hazard m tot and the total (i.e. overlapping) case-fatality hazards f X and f C are known. It follows that:
f X·πX = f X|~C·πX~C + f X|C·πXC, and
f C·πC = f C|~X·π~XC + f C|X·πXC. (40)
Following a derivation similar to that in eqs (19) – (21), one can show that, given total case-fatality hazards f X and f C, the case-fatality hazard for the joint condition is the sum of the conditional hazards:
f XC = f X|C + f C|X (41)
Further, since:
m X·T = f X|~C·(X ~ C) + f X|C·(XC), and
m C·T = f C|~X·(~XC) + f C|X·(XC), (42)
so:
m X = f X|~C·πX~C + f X|C·πXC, (43)
and:
m C = f C|~X·π~XC + f C|X·πXC. (44)
In other words, the cause-specific mortality hazards are weighted averages of the conditional case-fatality hazards, where weights are the proportions of the total population according to disease status regarding the other condition.
It remains true that:
m = m tot - m X - m C, (45)
as in eq. (27).
Other interactions
Another interaction might involve relaxing the assumption of independence between background mortality hazard m and case-fatality hazards f X and f C. However, in cases where such dependence is suspected or known, it may be possible to "work around" it by choosing appropriate definitions for X and C. For example, to take the ischaemic heart disease (X) and stroke (C) example, suppose it is important for the research question to account for the fact that individuals with X or C are also at increased risk of mortality from other selected causes of death such as cardiac failure. While one approach might be to introduce a new box for cardiac failure, within the current structure of PopMod, the onus is effectively on the analyst to take into account such increased risk of background mortality by modifying the way state C is defined and by adjusting the corresponding incidence and case-fatality rates. For example, state C could be defined as "stroke and all other conditions (including cardiac failure) at increased risk due to heart disease". Another type of exception to the general rule of independence between background mortality and cause-specific mortality would be the existence of any common causal modifiers of m, f X and f C, for example, the allocation of health-care expenditure.
Modelling mechanics
Initial conditions
PopMod describes population evolution conditional on initial conditions that define the state of the system at some initial time. These initial conditions consist of the population distribution in non-overlapping terms. If potentially overlapping populations (i.e. descriptions from the left hand side of Table 1) are considered, when the total prevalences p X and p C are known the non-overlapping population distribution can be fully determined by determining the prevalence of the joint group. Methods for this are discussed in the section Disease interactions.
Runge-Kutta method
The differential equation system is determined by its initial conditions and its parameters. An algebraic description of PopMod differential equation system – using notation from the right-hand side of Table 1 – is:
dS/dt = -(h S→X + h S→C + h S→D)·S + (h X→S)·X + (h C→S)·C (46a)
dX/dt = -(h X→S + h X→XC + h X→D)·X + (h S→X)·S + (h XC→X)·XC (46b)
dC/dt = -(h C→X + h C→XC + h C→D)·C + (h S→C)·S + (h XC→C)·XC (46c) (46)
dXC/dt = -(h XC→X + h XC→C + h XC→D)·XC + (h X→XC)·X + (h C→XC)·C (46d)
dD/dt = (h S→D)·S + (h X→D)·X + (h C→D)·C + (h XC→D)·XC (46e)
Under specified conditions, which apply here, such a differential equation system has a unique solution, and the solution can be expressed in terms of the eigenvalues and eigenvectors of the 5 × 5 coefficient matrix.[10]
Since finding the required eigenvalues and eigenvectors is here equivalent to solving a fifth-degree polynomial equation, specialized solution algorithms – and access to a substantial amount of processor time – will generally be required. An attractive alternative is therefore the use of numerical techniques, since they yield solutions more cheaply, and without requiring custom routines.
In PopMod, the evolution of the population in time is approximated by a 4th-order Runge-Kutta method, or, optionally, by a 5th-order Runge-Kutta method.[10] The relevant time step is defined as a fraction of the standard reporting interval (the number of divisions of the basic reporting interval must in principle be divisible by 3, but to allow for the possibility of starting with mid-year values in the first year, the number of divisions must be divisible by 6 and the minimum number of divisions is fixed at 12). Note that an nth-order numerical method will in general provide useful results so long as the differentials are smaller than nth-order in the chosen time step.
Each population age- and sex group is modelled as a separate system, and age is updated by taking end-of-year solution values for the "age = α " system as the initial values for the "age = α + 1" system in the subsequent model year.
A 4th-order Runge-Kutta method provides solutions to differential equations of the type:
dy i (x)/dx = f i (x, y i (x)), (47)
and is defined by the ansatz (Euler method) that:
y i (x + Δx) = y i (x) + Δx·f i (x, y i (x)), (48)
where:
y i (x + Δx) = y i (x) + (k 1i + 2k 2i + 2k 3i + k 4i )/6 + O(Δx5), and
k 1i = Δx·f i (x, y i )
k 2i = Δx·f i (x + Δx/2, y i + k 1i /2) (49)
k 3i = Δx·f i (x + Δx/2, y i + k 2i /2)
k 4i = Δx·f i (x + dx, y i + k 3i ).
Note that here x = t, y i = S, X, C, XC and D and that the differential equations (46a-46e) are not explicitly time dependent, that is, f i (t, y i (t)) = f i (y i (t)).[10]
Output interpretation
Standard PopMod output reports P(t) for each population group as end-of-interval (e.g. year-end) values, corresponding to the standard life table quantity l x . An important derived quantity also included in output is the time at risk experienced by the group during the interval (∫P(t) dt), corresponding to the life table quantity L x (sometimes called "life-years" or "person-years").
For a constant population, population time at risk is calculated P·Δt. For PopMod populations, population time at risk for the interval b - a is calculated:

When the quantity resulting from eq. (50) with units "person-years" is divided by the length of the time interval with units "years", average population size for the interval (
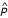
, with units "persons") is obtained:

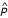
thus conforms to the definition of the expected value of the function P(t) on the interval b - a. Since b - a is by convention one year (or "chronon" etc.), the normalization to the interval b - a means dividing by 1. Thus, since in this case the numerical quantity is unchanged, substituting different reporting units yields two equally valid interpretations for the same output:
-
(1)
the average population size
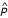
= E [P(t)] during the interval Δt, or
-
(2)
the population time at risk P LY experienced during the interval Δt.
Interpretation (1) also corresponds to average (count) prevalence for the population.
When transition rates are "small" (i.e. the differentials are approximately linear), average population can be interpreted as mid-interval population. Under the same assumptions, mid-year population provides a good estimate of population time at risk.
PopMod numerically evaluates P LY with a standard Newton-Cotes formula for 4-point closed quadrature, sometimes also called Simpson's 3/8-rule.[11] The quadrature formula relies on the values of P(t) determined by the Runge-Kutta method at multiples of the chosen time step. Since these values involve numerical estimation error, there is no simple expression for the order of accuracy of the different output values reported in PopMod.[10]
Discussion
Advantages of the approach
PopMod combines features of existing models (see below) with the possibility to analyse several disease states. It explicitly analyses time evolution and, even more importantly, abandons the constraint of independence of disease states.
A primary advantage of the approach adopted in PopMod is the separate modelling of age and time, and the type of bias inherent in models that do not do so has been previously pointed out.[7] Moreover, it has been independently noted that, without this feature, life-table measures are constrained to adopt – somewhat artificially – either a "period" or a "cohort" perspective.[6] The other chief advantage of PopMod is the ability to deal with heterogeneity of disease and mortality risk by modelling up to four disease states. No previous published generic population model has combined both these features. Note, however, that if disease conditions are independent, and population-dependent effects are not of interest, a multi-state life-table approach should probably be adopted.[20]
A further advantage of PopMod is the introduction of a systematic analytical approach to the modelling of disease interactions. This by itself represents a relatively important advance, as modellers have until now been constrained to model only independent conditions. Furthermore, in spite of the increased informational demands made by a four-state system, the modelled functional dependency between X-related hazards conditional on C status, and vice versa, reduces the number of exogenous hazards that need to be directly observed. This is of substantial practical importance, since, while direct observation of conditional hazards usually requires a cohort study, it will often be possible to obtain estimates of the required rate ratios from more common case-control studies [21].
Related models
In addition to the multi-state life table family,[3, 4] two additional families of mathematical models have some similarity to PopMod. One family comprises the class of models sometimes called incidence, prevalence and mortality (IPM) models.[12–14] Another family (with until now one member) is that of published population models, in particular Prevent.[15–18]
IPM models per se have no population or age structure; they can be conceived of as stationary population models (i.e. models of a population in equilibrium, where the numbers of births and deaths in an age group are equal). However, DisMod, probably the IPM model in most common use, [12] has gone through several versions, and the current version allows for hazard trend analysis that relies on modelling a full population structure based on one-year age groups. Notwithstanding, IPM models analyse only a single disease condition in isolation, and, while Prevent was explicitly designed to analyse a full population cohort structure, it also analyses only a single disease condition.
Multi-state life tables analyse multiple disease states but published versions have invariably required the assumption of independence across diseases. In addition, multi-state life tables implicitly impose a stationary population assumption by not independently modelling population time and age.
Averaging and its implications
In all compartmental models, of which differential equations models are one type, it is assumed that health and mortality risk are conditional on disease state. In light of the seemingly infinite diversity of real phenomena, this assumption invariably results in "compression", that is, the imposition of artificial homogeneity. In many cases, compression can be considered a necessary simplifying assumption for the modelling exercise, but in other cases, heterogeneity must be explicitly modelled to avoid the phenomenon of confounding. In a differential equations system, modelling heterogeneity of disease and mortality risk amounts to introducing additional disease states. Thus, PopMod, with four disease states, respresents a substantial increase in complexity over population models modelling only two disease states (e.g. diseased and healthy). PopMod of course includes the two-disease-state model as a special case.
There is also heterogeneity other than of disease and mortality risk. In particular, although real populations change in integer steps at discrete moments in time, a differential equation system represents this process in continuous time. However, this approximation is in general acceptably good when a large number of individuals comprise the population of interest. Moreover, an implication of representing age in a discrete number of statistical bins is modelling a birth-year cohort as though it had a single average age. If births are distributed uniformly throughout the year, the average birthday of the cohort is the mid-year point, and there is no serious objection to this procedure. However, if the cohort average birthday is not be the mid-year point, PopMod's modelled age will differ from the true average age.
It is assumed that conditional hazards are constant within a single reporting interval (e.g. one year), which will in principle be problematic for conditions with high initial case-fatality, for example heart attack (or stroke). This sort of problem can be addressed by defining condition C as ''acutely fatal cases'' and condition X as ''long-term survivors''. Similarly, for conditions of determinate duration (e.g. pregnancy), use of a constant hazard rate for ''remission'' will result in an exponential distribution of waiting time for transition out of the state, whereas a uniform distribution of waiting time is what would be wanted.
All compartmental population models are fundamentally simplifications of reality by means of a system of reduced dimensionality. The mathematical concept of "projection" is useful: the simplified system can be thought of as a "least-squares approximation" to the higher-order real system.[19] The validity of input parameter values and the accuracy of the solution method determine the actual goodness of fit realized in a particular model. Nevertheless, compression applies to every modelled variable in a differential equations model. Other modelling approaches, such as microsimulation, require much less compression, so the user who wishes to avoid compression systematically should consider adopting the microsimulation approach.
Types of error in PopMod
Sources of error in PopMod can be divided into three types:
-
(1)
Model (or "projection") error due to analysing a simplified system instead of the full one. Model error includes the characterization of scenarios for disease interaction.
-
(2)
Numerical error due to obtaining approximate solution values with numerical techniques.
-
(3)
Parameter error due to uncertainty about observed or derived parameter values.
The 5th-order Runge-Kutta method provides an estimate of the local truncation error inherent in the 4th-order numerical technique. Monte-Carlo analysis of distributions around transition rates can be used to examine parameter uncertainty. However, comparison with a more complex model would be necessary for quantification of model error. A way of investigating the impact of model error would be to construct progressively more realistic and complex models. A spectrum of models, from least to most complex, can thus be imagined, where the "most complex" and necessarily imaginary model has a one-to-one relation to real system it represents. The difference between the results of two adjacent models in such a series would be an expression of model error analogous to the estimate of numerical truncation error afforded by the next-higher-order numerical method.
Although intuitively natural and mathematically valid, in most situations it would be impractical to quantify model error in this laborious way. Nevertheless, model error may, in certain data-rich cases, be estimated by ''predicting'' outcomes for which numerical data are available for comparison but which are not used as inputs.
Limiting assumptions
Although any state transitions are in principle possible, PopMod assumes that transitions S→XC and X→C do not occur. This is because such transitions can be thought of as the simultaneous occurrence of two transitions (for example, S→XC equals S→X plus X→XC). Note that this does not imply events S→XC and X→C cannot occur within a single reporting interval; rather, it just means the mathematics of PopMod do not represent simultaneous events. A similar feature is the absence of a modelled cause of death "XC".
However, the non-modelled transition S→XC can be imagined if someone in state S simultaneously acquires X and C as a result of, say, very high levels of common risk factors (i.e. someone who suffers a simultaneous heart attack and stroke because of high blood pressure and cholesterol). If such a "simultaneous event" results in mortality, one could potentially speak of a cause of death "XC". Similarly, the non-modelled transition X→C could occur if there were "perfect interference" between two diseases such that acquiring C caused immediate remission from X. If either of these cases is important, PopMod can miss important dynamics.
Conflict of interest
None declared.
References
Shryock HS, Siegel JS: The life table. In: The methods and materials of demography (Edited by: Stockwell EG). Orlando, FL, Academic Press 1976, 250.
Hacking I: The emergence of probability. Cambridge, Cambridge University Press 1975.
Barendregt JJ, Bonneux L: Degenerative disease in an aging population: models and conjectures. Enschede, Netherlands, Febodruke 1998.
Manton KG, Stallard E: Chronic disease modelling. London, Charles Griffin 1988.
Schoen R: Modelling multigroup populations. New York and London, Plenum Press 1987.
Barendregt JJ: Incidence- and prevalence-based summary measures of population health (SMPH): making the twain meet. In: Summary measures of population health: concepts, ethics, measurement and applications (Edited by: Murray CJL, Lopez AD, Salomon JA, Mathers CD). Geneva, World Health Organization 2002, 221–231.
Preston SH: Health indices as a guide to health sector planning: a demographic critique. In: The epidemiological transition, policy and planning implications for developing countries (Edited by: Gribble JN, Preston SH). Washington DC, National Academy Press 1993.
Murray CJL: Rethinking DALYs. In: The Global Burden of Disease: A comprehensive assessment of mortality and disability from diseases, injuries, and risk factors in 1990 and projected to 2020 (Edited by: Murray CJ, Lopez AD). Cambridge, MA, Harvard University Press 1996, 1–98.
Anderson RM, May RM: Infectious diseases of humans: dynamics and control. Oxford, Oxford University Press 1991.
Lambert JD: Numerical methods for ordinary differential systems: the initial value problem. Chichester, Wiley 1991.
Ralston A, Rabinowitz P: A first course in numerical analysis. Mineola, NY, Dover 2 Edition 1965.
Kruijshaar ME, Barendregt JJ, Hoeymans N: The use of models in the estimation of disease epidemiology. Bull World Health Organ 2002, 80: 622–628.
Murray CJ, Lopez AD: Quantifying disability: data, methods and results. Bull World Health Organ 1994, 72: 481–494.
Barendregt JJ, Baan CA, Bonneux L: An indirect estimate of the incidence of non-insulin-dependent diabetes mellitus. Epidemiology 2000, 11: 274–279. 10.1097/00001648-200005000-00008
Mooy JM, Gunning-Schepers LJ: Computer-assisted health impact assessment for intersectoral health policy. Health Policy 2001, 57: 169–177. 10.1016/S0168-8510(00)00134-2
Bronnum-Hansen H: How good is the Prevent model for estimating the health benefits of prevention? J Epidemiol Community Health 1999, 53: 300–305.
Gunning-Schepers LJ: Models: instruments for evidence based policy. J Epidemiol Community Health 1999, 53: 263.
Bronnum-Hansen H, Sjol A: [Prediction of ischemic heart disease mortality in Denmark 1982–1991 using the simulation model Prevent]. Ugeskr Laeger 1996, 158: 4898–4904.
Strang G: Linear algebra and its applications. San Diego, CA, Harcourt Brace Jovanovich 3 Edition 1988.
Barendregt JJ, van Oortmarssen GJ, van Hout BA, Van Den Bosch JM, Bonneux L: Coping with multiple morbidity in a life table. Math Popul Stud 1998, 7: 29–49.
Rothman KJ, Greenland S: Modern epidemiology. Philadelphia, PA, Lippincott Williams and Wilkins 2 Edition 1998.
Acknowledgements
Reviewers Nico Nagelkerke of Leiden University and Louis Niessen of Erasmus University Rotterdam are gratefully acknowledged. Jan Barendregt and Sake de Vlas of Erasmus University Rotterdam also offered valuable comments and suggestions for revision. David Evans, Raymond Hutubessy, Stephen Lim, Colin Mathers, Sumi Mehta, Josh Salomon and Tessa Tan Torres of the World Health Organization, Geneva, are also gratefully acknowledged for their comments and contributions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
JL devised the methodology, implemented the conceptual and technical development of PopMod, including coordination of co-authors' contributions, and drafted and revised the manuscript. KR and HW contributed to the development of the methodology, drafted certain sections and revised the manuscript. CC and SG contributed to the development of the methodology, revised mathematical formulae throughout, and revised the manuscript. CM provided the initial idea for the model and also contributed technical modifications throughout development of the main ideas presented in this paper. All authors approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
About this article
Cite this article
Lauer, J.A., Röhrich, K., Wirth, H. et al. PopMod: a longitudinal population model with two interacting disease states. Cost Eff Resour Alloc 1, 6 (2003). https://doi.org/10.1186/1478-7547-1-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1478-7547-1-6

